CONJUNCIÓN (^)

La conjunción se presenta con los términos gramaticales: “y”, “pero”, “más”, “también”, “sin embargo”, “además”,

Signos de puntuación como: la coma, el punto, y el punto y coma.

Tabla de verdad de la Conjunción

REGLA.- La conjunción será verdadera solamente cuando el valor de verdad de ambas proposiciones es verdadero

si se tienen las proposiciones:

a:obtengo buenas notas

b:gano una beca

• la conjunción entre a y b es:

a^b:Obtenga buenas notas y gano una beca 

DISYUNCIÓN  (V)

La Disyunción se presenta con el término gramatical «o».

REGLA.- La Disyunción será falsa solamente cuando el valor de verdad de ambas proposiciones es falso.

ejemplo

Si se tienen las proposiciones:

                a: Tengo un libro de Trigonometría.

                b: Tengo un libro de Álgebra.

La disyunción entre a y b es:

avb: Tengo un libro de Trigonometría o uno de Álgebra.

CONDICIONAL

Viene a ser la combinación de dos proposiciones con “si… entonces”.

Se lee si p entonces q.

tabla de verdad de la condicional

REGLA.- Una proposición condicional es falsa cuando la primera proposición es verdadera y la segunda es falsa. Es verdadera en cualquiera de las otras formas

ejemplo:

si se tienen las proposiciones:

a:juan gana el concurso

b:juan dona $10 000

la condicional entre a y b es:

a→b: Juan dona $10 000 si gana el concurso

BICONDICIONAL

Es la unión de dos proposiciones por “si y sólo si”. Se lee a si y sólo si b.

REGLA.- Una proposición bicondicional es verdadera cuando, o sus dos componentes son verdaderos o sus dos componentes son falsos.

La flecha "↔" es el operador bicondicional. Ten en cuenta que, en la tabla de verdad, vemos que, para p↔q ser verdadera, ambas p y q deben tener los mismos valores de verdad; sí no, es falsa la conversa.

Algunas frases del BicondicionalCada uno de los siguientes es equivalente al bicondicional p↔q. p si y solo si q.p es necesario y suficiente para q. p es equivalente a q. Ten en cuenta que p↔q es lógicamente equivalente a q↔p (se le pedirá mostrar esto como un ejercicio), así que podemos invertir p y q en las frases de arriba.

Ejemplo 10 Bicondicional

(a) Verdad o falsa? "1+1 = 3 si y solo si Marte es un agujero negro."
(b) Reformula la oración: "Enseño matemáticas si y solo si me pagan una gran suma de dinero."

Solución

(a) Verdadera. La proposición dada tiene la forma p↔q, dónde p: "1+1=3" y q: "Marte es un agujero negro." Ya que ambas proposiciones son falsas, el bicondicional p↔q es verdadera.(b) Aquí están algunas maneras equivalentes de expresar esta oración:


"Enseñar matemática es necesario y suficiente para que me paguen una gran suma de dinero.""Me pagan una gran suma de dinero si y solo si enseño matemáticas."
Lamentablemente para nuestras finanzas, ninguna de las dos oraciones es verdad.

FORMA PROPOSICIONAL 

Son expresiones que se obtienen a combinar las variables proposicionales (p,q,r…..) con los conectivos lógicos(~,⋀,….).

A las formas proposicionales se denotan con las letras A, B, C, etc. En caso de que se quiera enfatizar las variables que intervienen en las funciones proposicionales se escribe: A(p,q).

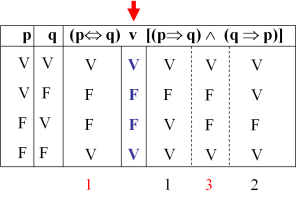
TAUTOLOGIA

Es una expresión lógica que resulta verdadera para cualquier interpretación; es decir, para cualquier asignación de valores de verdad.La construcción de una tabla de verdad es un método efectivo para determinar si una expresión cualquiera es una tautología o no.

EJEMPLO

CONTINGENCIA

Una proposición es una contingencia si no es ni verdadera ni falsa independientemente de los valores de verdad de las proposiciones simples que la componen.

Por ejemplo:

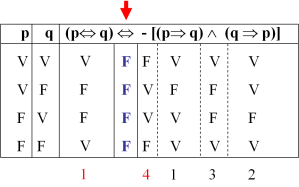
CONTRADICCIÓN 

Una proposición es una contradicción, si es falsa para todos sus valores de verdad .

Por ejemplo:

NOTA:para poder entender mejor pueden revisar estos videos que encontré en youtube 

Agrupación y Paréntesis

Son símbolos que usaremos para eliminar la ambigüedad cuando se trata de agrupar proposiciones. Para esto hacemos uso de paréntesis según ciertas convenciones con relación a los conectivos lógicos:

1. Una proposición negada será tratada como una proposición simple.
2. Si contiene sólo conectivos de un mismo tipo, agruparemos de izquierda a derecha.
3. Si posee varios conectivos diferentes agrupamos por el siguiente orden de prioridad:

Ejemplo:

1. p ↔ q ↔ r ↔ s ↔ t
   
   ( ( ( p ↔ q ) ↔ r ) ↔ s ) ↔ t


2. ¬p ∧ ¬q → t ∨  p ↔ q ∧ ¬r

Paso 1: ( ¬p ) ∧ ( ¬q ) →  t  ∨  p ↔ q ∧ (¬r )
se agrupan primero las proposiciones negadas, sin embargo no mantendremos los paréntesis por asuntos de legibilidad.
Paso 2: ( ¬p  ∧ ¬q ) →  t  ∨  p ↔ ( q ∧ ¬r )   se agrupan por las conjunciones.
Paso 3:  ( ¬p  ∧  ¬q ) → ( t  ∨  p ) ↔ ( q ∧¬r )  se agrupan por la disyunciones.
Paso 4: [ ( ¬p ∧ ¬q ) → ( t ∨  p ) ] ↔ ( q ∧¬r )   se agrupan por los condicionales.

Nos quedaría faltando el bicondicional pero ya todo quedo agrupado y no hay ambigüedad, ya no seria necesario colocar más paréntesis. 

Estos son algunos ejemplos que cumplen equivalencias lógicas y los cuales a su vez son leyes que usaremos para simplificar las expresiones lógicas:

ejemplo:

NOTA:para poder entender mejor pueden revisar estos videos que encontré en youtube 

RAZONAMIENTO

Razonamiento Llamaremos de esta forma a cualquier proposicion con la estructura 

P1 ∧ P2 ∧ · · · ∧ Pn −→ Q

 siendo n un entero positivo. A las proposiciones Pi , i = 1, 2, . . . , n se les llama premisas del razonamiento y a la proposici´on Q, conclusion del mismo. 

NOTA:para poder entender mejor pueden revisar estos videos que encontré en youtube