ECUACIONES

Una ecuación es un enunciado matemático que tiene dos expresiones separadas por un signo igual. La _expresión a la izquierda del signo igual tiene el mismo valor que la _expresión a la derecha.

Una o ambas expresiones pueden contener variables. Resolver una ecuación implica trabajar con las expresiones y encontrar el valor de las variables.

Ejemplo: 

Resolver la ecuación: 7x = 21 

Para que la ecuación se mantenga igual, debes aplicar la misma operación a ambos lados de la ecuación. Si multiplicamos (o dividimos)un lado por una cantidad, debemos multiplicar (o dividir) el otro lado por la misma cantidad. 

Esta ecuación se puede resolver dividiendo ambos lados por 7. 

La ecuación sería 7x/7 = 21/7. Esto se puede simplificar a x = 21/7 o x = 3. 

Puedes verificar tu cálculo sustituyendo el valor de x en la ecuación original. (7*3=21).

Ejemplo 2

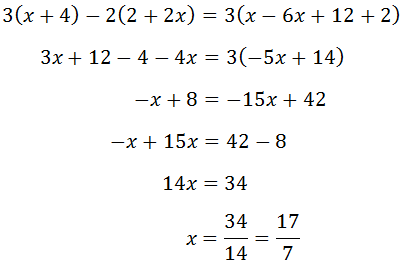Una ecuación de segundo grado es toda expresión de la forma:

ax² + bx +c = 0 con a ≠ 0.

Se resuelve mediante la siguiente fórmula:



ejemplos








 Por factorización

Este método consiste en resolver la ecuación como un producto de binomios, es decir encontrar dos números que multiplicados den como resultado “c” y sumados den “b”.

Este método se usa cuando a = 1.

Ejemplo:

x² + 3x – 18 = 0

Buscamos dos números que multiplicados den -18 y sumados 3, y nos encontramos con que el 6 y el -3 cumplen con estos requisitos…. 6 · (-3) = -18 y 6 + (-3) = 3


(x + 6)(x – 3) = 0
INECUACIONES 

Una inecuación es una expresión de la forma: f(x) < g(x), f(x) <= g(x), f(x) > g(x) o f(x)>= g(x).

La resolución de las inecuaciones es muy parecida a la resolución de las ecuaciones.

5x + 6 < 3x - 8
5x - 3x < -8 - 6
2x < -14
x < -7

Todos los valores de x menores que -7 satisfacen la inecuación.

Es muy importante tener en cuenta que si multiplicamos por un numero negativo una inecuación tenemos que cambiar el signo de la desigualdad.

3x > -2
-9x < 6
x < -2/3
Sistemas de inecuaciones de primer grado con una incógnita.

Se resuelven por separado las inecuaciones y se toman como soluciones los intervalos comunes de las soluciones

5x + 6 < 3x - 8
3x > 2

La solución de la primera ecuación es:

5x - 3x < -8 - 6
2x < -14
x < -7

La solución de la segunda ecuación es:

3x > -2
x < -2/3

La solución del sistema sería x < -7.

Inecuaciones de segundo grado.

Se resuelve como una ecuación de segundo grado y se estudian los signos que obtenemos con las soluciones.

x2 - 5x + 6 > 0

Las soluciones de la ecuación x2 - 5x + 6 = 0 son x = 3 y x = 2. Por lo tanto x2 - 5x + 6 = (x - 2)(x - 3).

Tenemos que estudiar los signos cuando x toma valores desde menos infinito hasta 2, desde 2 hasta 3 y desde 3 hasta infinito .

x - 2 es negativo para los valores entre menos infinito y 2.
x - 2 es positivo para los valores entre 2 y 3.
x - 2 es positivo para los valores entre 3 e infinito.
x - 3 es negativo para los valores entre menos infinito y 2.
x - 3 es negativo para los valores entre 2 y 3.
x - 3 es positivo para los valores entre 3 e infinito.

Por lo tanto, multiplicando los signos en los mismos intervalos:

x2 -5x + 6 es positivo para los valores entre menos infinito y 2.
x2 - 5x + 6 es negativo para los valores entre 2 y 3.
x2 - 5x + 6 es positivo para los valores entre 3 e infinito.  


NOTA: CON ESTE VÍDEO QUE ENCOTRE EN YOUTUBE PUEDE QUEDAR MAS CLARO EL TEMA DE LAS INECUACIONES 

RAZÓN Y PROPORCIÓN 

Razón

Una razón es una comparación entre dos o más cantidades. Puede expresarse mediante una fracción. Si las cantidades a comparar son  a y b, la razón entre ellas se escribe como:

Ejemplo:

En una sala de clases hay 10 mujeres y 18 hombres. ¿Qué relación numérica existe entre el número de mujeres y el número de hombres?

La relación entre el número de mujeres y el número de hombres es de  "10 es a 18" , otra forma de leerlo es "10 de 18 "

El término a es el antecedente de la razón y el b, el consecuente.

El resultado de la división o cociente entre el antecedente y el consecuente se denomina valor de la razón

Dos o más razones son equivalentes cuando tienen igual valor.

1.1- Resolución de problemas:

Veamos cómo resolver problemas de razones:

Ejemplo 1:

La edad de 2 personas están en la relación de 5 a 9 y la suma de ellas es 84. Hallar las edades.

Solución:

Si las edades son a y b

Cuando nos hablan de relación o razón entre dos cantidades sabemos que nos están hablando de una comparación entre dos cantidades. Por lo tanto expresamos los datos como una razón:

Ahora volvemos a los datos del problema:

Nos indican que la suma de los 2 números nos tiene que dar 84. Esto se expresa así:

Ahora lo que debemos hacer es trabajar con una constante, que en este caso será " X" . Por lo tanto :

Reemplazando los datos en la ecuación tenemos:

Ahora que tenemos el valor de x podemos reemplazar para obtener los valores de a y b :

Respuesta: Por lo tanto podemos decir que las edades son 30 y 54.

PROPORCIONALIDAD

Las magnitudes proporcionales pueden ser directamente proporcionales o inversamente proporcionales.

¿Cuándo son directamente proporcionales? Cuando al aumentar una de las magnitudes aumenta proporcionalmente la otra. Es decir, si al multiplicar o dividir una de ellas por un número, la otra también se multiplica o divide por ese mismo número.

Sin embargo, son inversamente proporcionales cuando al aumentar una de las magnitudes disminuye proporcionalmente la otra. Es decir, si al multiplicar una de ellas por un número la otra queda dividida por ese mismo número, o viceversa: si al dividir una de ellas entre un número la otra queda multiplicada por este número.

Problemas de proporcionalidad

Ahora vamos a ver algunos problemas de proporcionalidad, pensaremos si son de proporcionalidad directa o inversa y los resolveremos.

Al llegar al hotel nos han dado un mapa con los lugares de interés de la ciudad, y nos dijeron que 5 centímetros del mapa representaban 600 metros de la realidad. Hoy queremos ir a un parque que se encuentra a 8 centímetros del hotel en el mapa. ¿A qué distancia del hotel se encuentra este parque?

Para resolver este problema, debemos pensar en primer lugar si cumple una proporcionalidad directa o inversa. Para ello, pensamos…

Si en lugar de 5 centímetros hablásemos del doble de centímetros en el mapa (10 centímetros), ¿en la realidad serían más metros o menos metros?

Serían más metros: justo el doble de metros en la realidad.

Si al duplicar una magnitud (centímetros) también se duplica la otra (metros) estamos hablando de una proporcionalidad directa

Por lo tanto, vamos a resolver el problema:

Como 5 centímetros representan 600 metros, 1 centímetro representará…

600 : 5 = 120 metros

Como 1 centímetro representa 120 metros, 8 centímetros representarán…

120 x 8 = 960 metros

Solución: El parque se encuentra a 960 metros del hotel

Ayer 2 camiones transportaron una mercancía desde el puerto hasta el almacén. Hoy 3 camiones, iguales a los de ayer, tendrán que hacer 6 viajes para transportar la misma cantidad de mercancía del almacén al centro comercial. ¿Cuántos viajes tuvieron que hacer ayer los camiones?

Nos preguntamos si cumple una proporcionalidad directa o inversa. Para ello, pensamos…

Si en lugar de 3 camiones hablásemos del doble de camiones (6 camiones), ¿tendrían que hacer más o menos viajes?

 Cuantos más camiones carguen mercancía, en menos viajes se cargará toda: necesitarían justo la mitad de viajes

Si al duplicar una magnitud (camiones) se divide entre dos la otra (viajes necesarios) estamos hablando de una proporcionalidad inversa

Por lo tanto, vamos a resolver el problema:

Como 3 camiones necesitan hacer 6 viajes, 1 solo camión necesitaría hacer…

3 x 6 = 18 viajes

Como 1 solo camión necesitaría hacer 18 viajes, los 2 camiones tuvieron que hacer…

18 : 2 = 9 viajes

Solución: Ayer los 2 camiones hicieron 9 viajes cada uno

NOTA: ESTE VÍDEO LO ENCONTRÉ EN YOUTUBE Y ME PARECIÓ MUY BUENA LA EXPLICACIÓN 

Transformar decimal a fracción

Los números decimales pueden clasificarse en:

a) decimales finitos : son aquellos que tienen fin, es decir, no hay un número que se repita.

Ejemplos:  4,56 ;  0,0003 ;  2,9876 :  0,1 ;  3,42 , etc.

Siempre que se divida el numerador por el denominador, y la división termine y se obtenga resto cero , la división es exacta y su resultado será un decimal finito.

Un decimal finito representa una fracción decimal.

b) decimales infinitos : son aquellos números que no se acaban, es decir, hay uno o varios números que se repiten infinitamente. Por ejemplo: 0,333333.....  es infinito por que el 3 se repite indefinidamente . Estos números son divisiones inexactas. No representan una fracción decimal.

Los decimales infinitos pueden ser: infinitos puros, infinitos periódicos e infinitos semiperiódicos.

Al conjunto de los números racionales sólo pertenecen los números decimales infinitos periódicos y semiperiódicos. Los decimales infinitos puros pertenecen al conjunto de los números irracionales, porque no pueden transformarse en fracción.

c) decimales infinitos periódicos : son aquellos que tiene una o más cifras que se repiten sucesiva e infinitamente , formando el período . Se escribe en forma abreviada coronando al período con un pequeño trazo.

d) decimales infinitos semiperiódicos : En estos decimales aparecen una o más cifras antes del período. El número formado por dichas cifras se llama anteperíodo (es un número que está entre la coma y la rayita).

Transformación de un decimal finito a fracción

Se convierte el número a fracción decimal y, si se puede, se simplifica. Para transformar el número decimal a fracción decimal se utilizan potencias de diez (10, 100, 1.000, etc.). Se colocan tantos ceros como cifras decimales tenga el número.

Ejemplo 1:

Se anota el número, en este caso 45.  Se divide por 1.000,  porque  hay tres espacios decimales ocupados, luego simplificamos por 5

Ejemplo 2:

ransformación de un decimal infinito periódico en fracción

Los pasos a seguir son los siguientes:

1) Se anota el número y se le resta él o los números que están antes del período (de la rayita)

2) Se coloca como denominador un 9 por cada número que está en el período (si hay un número bajo la rayita se coloca un 9, si hay dos números bajo el período se coloca 99, etc.). Si se puede simplificar, se simplifica.

Otro ejemplo: Expresar como fracción 57,18181818....

Transformación de decimal infinito semiperiódico a fracción

1) El numerador de la fracción se obtiene , al igual que en el caso anterior, restando al número la parte entera y el anteperíodo, o sea, todo lo que está antes de la “rayita”.

2) El denominador de la fracción se obtiene colocando tantos 9 como cifras tenga el período y tantos 0 como cifras tenga el anteperíodo. Como siempre, el resultado se expresa como fracción irreductible (no se puede simplificar más) o como número mixto.

Operaciones 

PASO 1: Realizar las operaciones que estén dentro de los paréntesis.

En nuestro ejemplo, tenemos dentro del paréntesis una operación de suma que debemos de resolver en primer lugar.

PASO 2. Realizar las multiplicaciones  y divisiones que aparezcan.

Siguiendo con nuestro ejemplo de operaciones combinadas, ahora tenemos que realizar la operación de multiplicar:

PASO 3. Realizar las sumas y las restas que aparezcan.

Tan solo nos queda una resta para resolver la operación. Y el resultado es 38

OPERACION COMPLEJA 

Las fracciones complejas son fracciones en las que el numerador, el denominador o ambos términos contienen fracciones a su vez. Por este motivo, hay quien las llama "fracciones compuestas". Simplificar fracciones complejas es un proceso que puede ser sencillo o difícil, en base al número de términos que haya en el numerador y en el denominador, a que haya términos variables o no y, si los hay, a la complejidad de los términos variables. Lee el paso 1 para empezar.

Si es necesario, simplifica el numerador y el denominador para que haya una sola fracción en cada término. Las fracciones complejas no tienen por qué resultar difíciles de resolver. De hecho, las fracciones complejas en las que tanto el numerador como el denominador contienen una sola fracción suelen ser bastante fáciles de resolver. Por lo tanto, si el numerador o el denominador de la fracción compleja (o ambos términos) contienen varias fracciones o una combinación de fracciones y números enteros, simplifica el término para que quede una sola fracción tanto en el numerador como en el denominador. Puede que tengas que hallar el mínimo común denominador (MCD) de dos o más fracciones.

• Por ejemplo, supongamos que queremos simplificar la fracción compleja (3/5 + 2/15)/(5/7 - 3/10). Primero, simplificaríamos tanto el numerador como el denominador de la fracción compleja para que quede una sola fracción en cada término.
  • Para simplificar el numerador, utilizaremos u MCD de 15 multiplicando 3/5 por 3/3. El numerador se convertirá en 9/15 + 2/15 y, después de operar, en 11/15.
  • Para simplificar el denominador, utilizaremos un MCD de 70 multiplicando 5/7 por 10/10 y 3/10 por 7/7. El denominador se transformará en 50/70 - 21/70 y, después de operar, en 29/70.
  • Por lo tanto, la nueva fracción compleja será (11/15)/(29/70).

Invierte el denominador para hallar su inverso. Por definición, dividir un número entre otro es lo mismo que multiplicar el primer número por el inverso del segundo. Ahora que ya hemos obtenido una fracción compleja con una sola fracción tanto en el numerador como en el denominador, podemos utilizar esta propiedad de la división para simplificar la fracción compleja. Primero, halla el inverso de la fracción del denominador de la fracción compleja. Hazlo invirtiendo la fracción; es decir, colocando el numerador en lugar del denominador y viceversa.

• • • En el ejemplo con el que estamos trabajando, la fracción del denominador de la fracción compleja (11/15)/(29/70) es 29/70. Para hallar su inverso, simplemente le "damos la vuelta", obteniendo 70/29.
      • Ten en cuenta que, si la fracción compleja tiene un número entero en el denominador, puedes expresarlo como una fracción y hallar su inverso de la misma forma. Por ejemplo, si la fracción compleja fuese (11/15)/(29), podemos definir el denominador como 29/1, cuyo inverso sería 1/29.
  • 
  • Siempre que sea posible, utiliza el método del inverso multiplicativo explicado arriba. Para ser claros, prácticamente cualquier fracción compleja se puede simplificar reduciendo su numerador y su denominador a fracciones simples y multiplicando el numerador por el inverso del denominador. Las fracciones complejas con variables no son una excepción, aunque cuanto más complicadas sean las expresiones variables, más difícil será utilizar el inverso multiplicativo y más tiempo llevará. Para resolver fracciones complejas "sencillas" con variables, usar el inverso multiplicativo es una buena opción, pero para resolver las fracciones complejas con varias variables en el numerador y en el denominador puede que sea más fácil usar el método que describiremos a continuación.
    ·         Por ejemplo, (1/x)/(x/6) es fácil de simplificar con el inverso multiplicativo. 1/x × 6/x = 6/x². Aquí, no hay necesidad de utilizar ningún método alternativo.
    ·         Sin embargo, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))) es más difícil de simplificar con el inverso multiplicativo. Reducir el numerador y el denominador de esta fracción compleja para que quede una sola fracción en cada término, multiplicar por el inverso y reducir el resultado a una expresión lo más sencilla posible sería un proceso bastante complicado. En este caso, puede ser más fácil usar el método alternativo que ahora explicaremos.
     

si no es práctico usar el método del inverso multiplicativo, empieza hallando el mínimo común denominador de las fracciones de cada término de la fracción compleja. El primer paso en este método alternativo de simplificación es hallar el MCD de todas las fracciones que haya en los términos de la fracción compleja (tanto en el numerador como en el denominador. Normalmente, si una o varias fracciones tienen variables en sus denominadores, su MCD es simplemente el producto de sus denominadores.

• Esto es más fácil de comprender a través de un ejemplo. Intentemos simplificar la fracción compleja que hemos mencionado antes, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))). Las fracciones de los términos de la fracción compleja son (1)/(x+3) y (1)/(x-5). El denominador común de estas dos fracciones es el producto de sus denominadores: (x+3)(x-5).

En el video se establece la definición de una fracción compleja o compuesta como una fracción en que en el numerador o denominador contienen fracciones. Se discute dos procedimientos de cómo llevar una fracción compleja a una fracción simple, es decir a una fracción en que el numerador y denominador no contenga fracciones algebraicas.. El primero consiste en hacer las operaciones del numerador y denominador para luego efectuar la división de fracciones. El segundo procedimiento consiste en multiplicar numerador y denominador por el mínimo común múltiplo de los denominadores.

NOTA: ESTE VIDEO LO ENCONTRE EN YOUTUBE  ESTA MUY BIEN EXPLICADO

unidad 3 

Números reales

Los números reales son los que pueden ser expresados por un número entero (3, 28, 1568) o decimal (4,28; 289,6; 39985,4671). Esto quiere decir que abarcan a los números racionales (que pueden representarse como el cociente de dos enteros con denominador distinto a cero) y los números irracionales (los que no pueden ser expresados como una fracción de números enteros con denominador diferente a cero).

Los números naturales

Con los números naturales  contamos los elementos de un conjunto (numero cardinal). O bien expresamos la posición u orden que ocupa un elemento en un conjunto (ordinal).
El conjunto de los números naturales está formado por:

N= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}

La suma y el producto de dos números naturales es otro número natural.

La diferencia de dos números naturales no siempre es un número natural, sólo ocurre cuando el minuendo es mayor que sustraendo.

5 − 3

3 − 5

El cociente de dos números naturales no siempre es un número natural, sólo ocurre cuando la división es exacta.

6 : 2

2 : 6

Podemos utilizar potencias, ya que es la forma abreviada de escribir un producto formado por varios factores iguales.

La raíz de un número natural no siempre es un número natural, sólo ocurre cuando la raíz es exacta.

Los números enteros

Los números enteros son del tipo:

= {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}

Nos permiten expresar: el dinero adeudado, la temperatura bajo cero, las profundidades con respecto al nivel del mar, etc.

La suma, la diferencia y el producto de dos números enteros es otro número entero.

El cociente de dos números enteros no siempre es un número entero , sólo ocurre cuando la división es exacta.

6 : 2

2 : 6

Podemos operar con potencias, pero el exponente tiene que ser un número natural.





La raíz de un número entero no siempre es un número entero, sólo ocurre cuando la raíz es exacta o si se trata de una raíz de índice par con radicando positivo.


Los números racionales

Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero.

Los números decimales (decimal exacto, periódico puro y periódico mixto) son números racionales; pero los números decimales ilimitados no.

La suma, la diferencia , el producto y el cociente de dos números racionales es otro número racional.

Podemos operar con potencias, pero el exponente tiene que ser un número entero.

La raíz de un número racional no siempre es un número racional, sólo ocurre cuando la raíz es exacta y si el índice es par el radicando ha de ser positivo.

Los números irracionales

Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción.

El número irracional más conocido es , que se define como la relación entre la longitud de la circunferencia y su diámetro.

= 3.141592653589...

Otros números irracionales son:

El número e aparece en procesos de crecimiento, en la desintegración radiactiva, en la fórmula de la catenaria, que es la curva que podemos apreciar en los tendidos eléctricos.

e = 2.718281828459...

El número áureo, , utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus obras.

Números reales

El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por .

Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo y la división por cero.
La recta real

A todo número real le corresponde un punto de la recta y a todo punto de la recta un número real.





Números imaginarios

Un número imaginario se denota por bi, donde :

b es un número real

i es la unidad imaginaria:

Los números imaginarios permiten calcular raíces con índice par y radicando negativo.

x2 + 9 = 0

Números complejos

Un número complejo en forma binómica es a + bi.

El número a es la parte real del número complejo.

El número b es la parte imaginaria del número complejo.


Si b = 0 el número complejo se reduce a un número real, ya que a + 0i = a.

Si a = 0 el número complejo se reduce a bi, y se dice que es un número imaginario puro.

El conjunto de los números complejos se designa por .

Teorema fundamental de la aritmética

Todo número compuesto se puede descomponer de manera única como el producto de números primos.

Esta representación es única, salvo el orden de los factores.

Ejemplo: 1001 se puede escribir como producto de primos de forma única, como  .

Ejemplo: 24 se puede escribir como producto de primos de forma única, como  .

Ejemplo: El número de divisores de 1001 es  .

Ejemplo: El número de divisores de 24 es  .

Ejemplo: -1001 se puede escribir, salvo el signo como producto de primos de forma única, como -1001 = - (7x11x13).

Ejemplo: El número de divisores positivos de -1001 es t (1001) = 8.