"La esencia de las matemáticas no es hacer las cosas simples complicadas, sino hacer las cosas complicadas simples.-S. Gudder."

UNIDAD 1

Lógica matemática

Estudia la forma del razonamiento. 

Disciplina que por medio de reglas y técnicas determina si un argumento es o no válido.

1.1. Proposiciones

Una proposición es un enunciado u oración que puede ser verdadera o falsa, pero no las dos a la vez. ejemplo:

• Hoy es lunes (proposición)
• ¡socorro! ( no es proposición)

nota: las oraciones afirmativas,aseverativas,informativas,descriptivas son

proposiciones mientras que las oraciones exclamativas ,interrogativas e 

imperativas no lo son.

valor de verdad 

es la cualidad de veracidad que describe adecuadamente la proposición y puede ser verdadero o falso

• verdadero 1;V;T
• Falso         0;F;False

Ejm:
a:Guayaquil capital económica del Ecuador (1)
b:Juan vive en Milagro      (1)

TABLA DE VERDAD

Una tabla de verdad es una representación de los posibles valores de verdad que podría tomar una proposición.

Las tablas de verdad sirven para mostrar los valores, las relaciones y los resultados posibles al realizar operaciones lógicas.

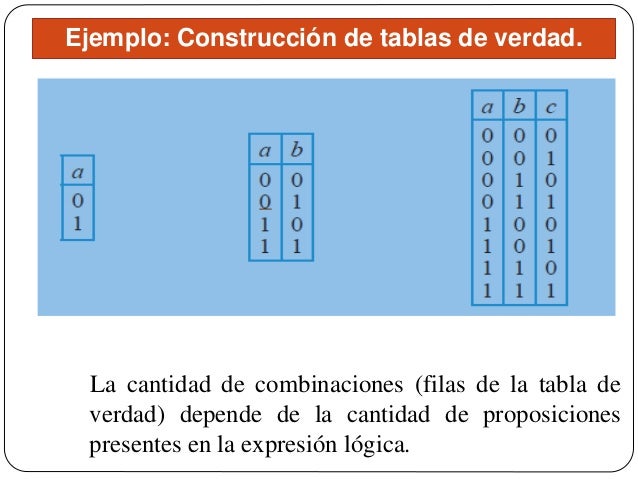
Ejemplo: Construcción de tablas de verdad.

En general para “n” proposiciones, se pueden presentar 2n posibilidades

FORMAS DE CONSTRUCCIÓN DE TABLAS DE VERDAD:

Paso 1: colocar las combinaciones de valores de verdad debajo de cada variable.
La fórmula del calculo es 2n (la n va arriba del 2) donde: * 2= representa los valores de certeza ( V o F).
* n = número de proposiciones atómicas.

[ ( P ^ Q) ——> (¬ P)] v ( ¬ Q)
Tenemos dos variables P y Q
Entonces 2 al cuadrado = 4

P Q

V V
V F
F V
F F

Paso 2: Transformar los valores de verdad tomando en cuenta la negación (si los hay)

Ejemplo: [ ( P ^ Q)—–> (¬P)] v (¬ Q)

¬ P ¬ Q

F F
F V
V F
V V

Paso 3: Se calula primero el calor de verdad de los paréntesis tomando en cuenta las definiciones del conectivo lógico.

Ejemplo: [( P ^ Q)—-> (¬ P)] v (¬Q)

P ^ Q

V
F
F
F

Paso 4: Se compara el resultado del valor de verdad del paréntesis con el valor de verdad del corchete (si lo hay)

Paso 5: Se compara el resultado de ese valor de verdad del corchete con el de las llaves (si lo hay)

(P ^ Q)—–> (¬P) [(P ^ Q)—-> ¬P] v¬Q

F F
V V
V V
V V

Luego de haber cumplido con esta serie de pasos habremos obtenido un resultado en la columna final de nuestra tabla de verdad la cual podremos calificarla como una teutologia, contingencia o contreadicción.